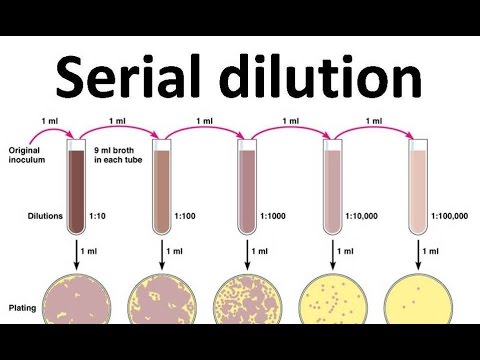
A serial dilution is the stepwise dilution of a substance in solution. Usually the dilution factor at each step is constant, resulting in a geometric progression of the concentration in a logarithmic fashion. A ten-fold serial dilution could be 1 M, 0.1 M, 0.01 M, 0.001 M ... Serial dilutions are used to accurately create highly diluted solutions as well as solutions for experiments resulting in concentration curves with a logarithmic scale. A tenfold dilution for each step is called a logarithmic dilution or log-dilution, a 3.16-fold (100.5-fold) dilution is called a half-logarithmic dilution or half-log dilution, and a 1.78-fold (100.25-fold) dilution is called a quarter-logarithmic dilution or quarter-log dilution. Serial dilutions are widely used in experimental sciences, including biochemistry, pharmacology, microbiology, and physics.
Serial dilution examples Serial dilutions are a common practice in the natural sciences. Due to the period decrease in concentration, this method is very useful when performing many types of experiments, from chemistry to biology to medicine.
In biology and medicine[edit]
In biology and medicine, besides the more conventional uses described above, serial dilution may also be used to reduce the concentration of microscopic organisms or cells in a sample. As, for instance, the number and size of bacterial colonies that grow on an agar plate in a given time is concentration-dependent, and since many other diagnostic techniques involve physically counting the number of micro-organisms or cells on specials printed with grids (for comparing concentrations of two organisms or cell types in the sample) or wells of a given volume (for absolute concentrations), dilution can be useful for getting more manageable results.[1] Serial dilution is also a cheaper and simpler method for preparing cultures from a single cell than optical tweezers and micromanipulators.[2]
- Titration of microorganisms in infectious or environmental samples is a corner stone of quantitative microbiology. A simple method is presented to estimate the microbial counts obtained with the serial dilution technique for microorganisms that can grow on bacteriological media and develop into a colony.
- Serial dilution examples. Serial dilutions are a common practice in the natural sciences. Due to the period decrease in concentration, this method is very useful when performing many types of experiments, from chemistry to biology to medicine.You can plot the information they provide onto a graph to find the gradient and intercepts, so that information about any trends can be spotted.
In homeopathy[edit]
Serial dilution is one of the core foundational practices of homeopathy, with 'succussion', or shaking, occurring between each dilution. In homeopathy, serial dilutions (called potentisation) are often taken so far that by the time the last dilution is completed, no molecules of the original substance are likely to remain.[3][4]
See also[edit]
References[edit]
- ^K. R. Aneja. Experiments in Microbiology, Plant Pathology and Biotechnology. New Age Publishers, 2005, p. 69. ISBN81-224-1494-X
- ^Booth, C.; et al. (2006). Extremophiles. Methods in microbiology 35. Academic Press. p. 543. ISBN978-0-12-521536-7.
- ^Weissmann, Gerald (2006). 'Homeopathy: Holmes, Hogwarts, and the Prince of Wales'. The FASEB Journal. 20 (11): 1755–1758. doi:10.1096/fj.06-0901ufm. PMID16940145. Retrieved 2008-02-01.
- ^Ernst, Edzard (November 2005). 'Is homeopathy a clinically valuable approach?'. Trends in Pharmacological Sciences. 26 (11): 547–548. CiteSeerX10.1.1.385.5505. doi:10.1016/j.tips.2005.09.003. PMID16165225.
- Michael L. Bishop, Edward P. Fody, Larry E. Schoeff. Clinical Chemistry: Principles, Procedures, Correlations. Lippincott Williams & Wilkins, 2004, p. 24. ISBN0-7817-4611-6.
External links[edit]
- How to Make Simple Solutions and Dilutions, Bates College
October 2010
Author: Robert Blodgett (retired)
For additional Information, contact: Stuart Chirtel or Guodong Zhang
Serial Dilution Procedure Ppt
Revision History:
- April 2015: Contact for this Appendix was updated
- October 2010: Equation for most probable number (MPN) replaced with graphical version; Added expanatory note for the downloadable spreadsheet.
- July 2003: Added Table 5. for 10 tubes at 10 ml inocula and link to spreadsheet.
Background
References
Tables
Background
Serial dilution tests measure the concentration of a target microbe in a sample with an estimate called the most probable number (MPN). The MPN is particularly useful for low concentrations of organisms (<100/g), especially in milk and water, and for those foods whose particulate matter may interfere with accurate colony counts. The following background observations are adapted and extended from the article on MPN by James T. Peeler and Foster D. McClure in the Bacteriological Analytical Manual (BAM), 7th edition.
Only viable organisms are enumerated by the MPN determination. If, in the microbiologist's experience, the bacteria in the prepared sample in question can be found attached in chains that are not separated by the preparation and dilution, the MPN should be judged as an estimate of growth units (GUs) or colony-forming units (CFUs) instead of individual bacteria. For simplicity, however, this appendix will speak of these GUs or CFUs as individual bacteria. If a confirmation test involves selecting colonies to test, then a statistical adjustment not discussed in this appendix should be used (see Blodgett 2005a.)
The following assumptions are necessary to support the MPN method. The bacteria are distributed randomly within the sample. The bacteria are separate, not clustered together, and they do not repel each other. Every tube (or plate, etc.) whose inoculum contains even one viable organism will produce detectable growth or change. The individual tubes of the sample are independent.
The essence of the MPN method is to dilute the sample to such a degree that inocula in the tubes will sometimes but not always contain viable organisms. The 'outcome', i.e., the number of tubes and the number of tubes with growth at each dilution, will imply an estimate of the original, undiluted concentration of bacteria in the sample. In order to obtain estimates over a broad range of possible concentrations, microbiologists use serial dilutions incubating tubes at several dilutions.
The MPN is the number which makes the observed outcome most probable. It is the solution for λ, concentration, in the following equation
where exp(x) means ex, and
K denotes the number of dilutions,
gj denotes the number of positive (or growth) tubes in the jth dilution,
mj denotes the amount of the original sample put in each tube in the jth dilution,
tj denotes the number of tubes in the jth dilution.
In general, this equation can be solved by iteration.
McCrady (1915) published the first accurate estimation of the number of viable bacteria by the MPN method. Halvorson and Ziegler (1933), Eisenhart and Wilson (1943), and Cochran (1950) published articles on the statistical foundations of the MPN. Woodward (1957) recommended that MPN tables should omit those combinations of positive tubes (high for low concentrations and low for high concentrations) that are so improbable that they raise concerns about laboratory error or contamination. De Man (1983) published a confidence interval method that was modified to make the tables for this appendix.
Confidence Intervals
The 95 percent confidence intervals in the tables have the following meaning:
Before the tubes are inoculated, the chance is at least 95 percent that the confidence interval associated with the eventual result will enclose the actual concentration.
It is possible to construct many different sets of intervals that satisfy this criterion. This manual uses a modification of the method of de Man (1983). De Man calculated his confidence limits iteratively from the smallest concentrations upward. Because this manual emphasizes pathogens, the intervals have been shifted slightly upward by iterating from the largest concentrations downward.
The confidence intervals of the spreadsheet and the tables associated with this appendix may be different. The MPN Excel spreadsheet uses a normal approximation to the log (MPN) to calculate its confidence intervals. This approximation is similar to a normal approximation discussed in Haldane (1939). This approximation is less computationally intense so more appropriate for a spreadsheet than de Man's confidence intervals.
Precision, Bias, and Extreme Outcomes
The MPNs and confidence limits have been expressed to 2 significant digits. For example, the entry '400' has been rounded from a number between 395 and 405.
Numerous articles have noted a bias toward over-estimation of microbial concentrations by the MPN. Garthright (1993) has shown, however, that there is no appreciable bias when the concentrations are expressed as logarithms, the customary units used for regressions and for combining outcomes. Therefore, these MPNs have not been adjusted for bias.
The outcome with all positive tubes in each dilution gives no upper bound on the concentration. The tables in this appendix list the MPN for this outcome as greater than the highest MPN for an outcome with at least one negative tube. Similarly, the outcome with all negative tubes is listed as less than the lowest MPN for an outcome with at least one positive tube.
Cautionary Notes
Improbable Outcomes
Several potential problems may cause improbable outcomes. For example, there may be interference at low dilutions or selecting too few colonies at low dilutions for a confirmation test may overlook the target microbe. If the problem is believed limited to the low dilutions, then using only the high dilutions with positive tubes might be more reliable. If the cause of the problem is unknown, then the estimate may be unreliable.
When excluding improbable outcomes, de Man's (1983) preferred degree of improbability was adopted. The outcomes included are among the 99.985 percent most likely outcomes if their own MPNs were the actual bacterial concentrations. Therefore, among 10 different outcomes, all will be found in these tables at least 99 percent of the time.
Inconclusive Tubes
In special cases where tubes cannot be judged either positive or negative (e.g., plates overgrown by competing microflora at low dilutions), these tubes should be excluded from the outcome. The resulting outcome may have different numbers of tubes than any of the tables in this appendix. Its MPN can be solved by computer algorithms or estimated by Thomas's Rule below. Haldane's method can find the confidence limits as described below Thomas's rule.
Using Tables
Selecting Three Dilutions for Table Reference
An MPN can be computed for any positive number of tubes at any positive number of dilutions, but often serial dilutions use three or more dilutions and a decimal series (Each dilution has one tenth as much of the original sample as the previous dilution.) The tables in this appendix require reducing an outcome to three of its decimal dilutions. This procedure for selecting three dilutions was developed for the designs (numbers of tubes per dilution and ratio of dilutions) in these tables. They all have decimal dilutions and a fairly small number of tubes per dilution. For other designs, other procedures may be needed. When the MPN model holds, the three decimal dilutions are chosen to give a good approximation to the MPN of the entire outcome. Otherwise, the reduction may remove interference (possible from another species of microbe or a toxic substance) that can be diluted out. The remainder of this section tells how to select the three dilutions.
First, remove the highest dilution (smallest sample volume) if it and the next lower dilution have all negative tubes. As long as this condition holds and at least four dilutions remain, continue removing these dilutions.
Next, if only three dilutions remain, use them as illustrated in example A. In each example there are five tubes in each dilution. In example A, removing the two highest dilutions (0.001 and 0.01 grams) leaves three dilutions.
If more than three dilutions remain, then find the highest dilution with all positive tubes. There are three cases. In the first case, the highest dilution with all positive tubes is within the three highest remaining dilutions. Then use the three highest remaining dilutions. In example B, the first step removes the highest dilution (0.001 grams.) Since the highest dilution with all positive tubes (1 gram) is within the three highest remaining dilutions, (1, 0.1, and 0.01 grams,) use them. In example C, the highest dilution with all positive tubes (0.01 g) is within the three highest remaining dilutions (0.1, 0.01, and 0.001.)
In the second case, the highest dilution with all positive tubes is not within the three highest remaining dilutions. Then select the next two higher dilutions than the highest dilution with all positive tubes. Assign the sum of the positive tubes of any still higher dilutions to the third higher dilution. In example D, the highest dilution with all positive tubes has 1 gram. Select the two dilutions immediately higher which have 0.1 and 0.01 grams. There is only one higher dilution whose positive tubes are assigned to form the third dilution with 0.001 grams.
In the third case, there is no dilution with all positive tubes. Then select the two lowest dilutions. Assign the sum of the positive tubes of any higher dilutions to the third dilution. In example E no dilution has all positive tubes. The two lowest dilutions have 10 and 1 grams. The sum of the positive in the dilutions with 0.1, 0.01 and 0.001 grams is assigned to form the third dilution with 0.1 grams.
If the three dilutions selected are not in the tables, then something in the serial dilution probably was unusual. This is a warning that the outcome is sufficiently improbable that the basic assumptions of the MPN may be questionable. If possible, redoing the test may be the most reliable procedure. If an MPN value is still desired, use the three highest remaining dilutions. In example F, the three highest dilutions are used. If these dilutions are not in the tables, then use the highest dilution with any positive tubes. The section entitled 'MPN for a single dilution with any positive tubes' shows how to calculate the MPN.
| Examples | 10 g | 1 g | .1 g | .01 g | .001 g | |
|---|---|---|---|---|---|---|
| A | 4 | 1 | 0 | 0 | 0 | 410xx |
| B | 5 | 5 | 1 | 0 | 0 | x510x |
| C | 4 | 5 | 4 | 5 | 1 | xx451 |
| D | 4 | 5 | 4 | 3 | 1 | xx431 |
| E | 4 | 3 | 0 | 1 | 1 | 432xx |
| F | 4 | 3 | 3 | 2 | 1 | xx321 |
Conversion of Table Units
The tables below apply to inocula of 0.1, 0.01, and 0.001 g. When different inocula are selected for table reference, multiply the MPN/g and confidence limits by whatever multiplier makes the inocula match the table inocula. For example, if the inocula were 0.01, 0.001, and 0.0001 with three tubes per dilution, multiplying by 10 would make these inocula match the table inocula. If the outcome were (3, 1, 0), multiply the Table 1 MPN/g estimate, 43/g, by 10 to arrive at 430/g.
Bounds and approximations for a design without a table
The MPN for a serial dilutions not addressed by any table (e.g., resulting from accidental loss of some tubes) may be computed by iteration or bounded as follows.
Where W and Q are two disjoint sets of dilutions that together contain all the dilutions. The lower bound allows low dilutions with all positive tubes to be deleted from the bound. Blodgett (2005b) introduces these and other bounds.
The following gives an estimate of the MPN. First, select the lowest dilution that doesn't have all positive tubes. Second, select the highest dilution with at least one positive tube. Finally, select all the dilutions between them. Use only the selected dilutions in the following formula of Thomas (1942):
MPN/g = (∑ gj) / (∑ tjmj ∑ (tj-gj)mj) (½)
where the summation is over the selected dilutions and
∑ gj denotes the number of positive tubes in the selected dilutions,
∑ tjmj denotes the grams of sample in all tubes in the selected dilutions,
∑ (tj-gj)mj denotes the grams of sample in all negative tubes in the selected dilutions.
The following examples will illustrate the application of Thomas's formula. We assume that the dilutions are 1.0, 0.1, 0.01, 0.001, and 0.0001 g.
Example (1). For outcome (5/5, 10/10, 4/10, 2/10, 0/5) use only (–,–, 4/10, 2/10,–); so ∑ tjmj = 10*0.01 + 10*0.001 = 0.11. Where * means multiplication. There are 6 negative tubes at 0.01 and 8 negative tubes at 0.001, so ∑ (tj-gj)mj = 6*0.01 + 8*0.001 = 0.068. There are 6 positive tubes, so
MPN/g = 6/(0.068 * 0.11)(½) = 6/0.086 = 70/g
Example (2). For outcome (5/5, 10/10, 10/10, 0/10, 0/5) use only(–, –, 10/10, 0/10,–), so by Thomas's formula,
MPN/g = 10/(0.01 * 0.11)(½) = 10/.0332=300/g
These two approximated MPNs compare well with the MPNs for (10, 4, 2) and (10,10,0) (i.e., 70/g and 240/g, respectively).
Approximate confidence limits for any dilution test outcome can be calculated by first estimating the standard error of log10(MPN) by the method of Haldane. We describe the method for 3 dilutions, but it can be shortened to 2 or extended to any positive number.
Let m1, m2, m3 denote the inoculation amounts at the largest to the smallest amounts (e.g., m1 = 0.1 g, m2 = 0.01 g, m3 = 0.001 g in these tables).
Let g1, g2, g3 denote the numbers of positive tubes at the corresponding dilutions. For legibility, we denote yx by 'y**x' and 'y times x' by 'y*x'.
Now we compute
T1 = exp(-mpn*m1), T2 = exp(-mpn*m2), etc.
Then we compute
B = [g1*m1*m1*T1/((T1 - 1)**2] + ... + [g3*m3*m3*T3/((T3 - 1)**2)].
Finally, we compute
Standard Error of Log10(mpn) = 1/(2.303*mpn*(B**0.5))
Now the 95 percent confidence intervals, for example, are found at
Log10(mpn) ± 1.96*(Standard Error).
MPN for a Single Dilution with any Positive Tubes
If just one dilution has any positive tubes, then a simpler expression gives its MPN.
MPN/g = (1/m)*2.303*log10((∑ tjmj)/(∑ (tj-gj)mj))
Where m denotes the amount of sample in each tube in the dilution with a positive tube.
Special requirements and tables included
The attached spreadsheet should be able to handle most specialized designs. Garthright and Blodgett (2003) discusses this spreadsheet. Requests for special computations and different designs will be honored as resources permit. Designs may be requested with more or less than 3 dilutions, uneven numbers of tubes, different confidence levels, etc. (Telephone 301-436-1836 or write the Division of Mathematics, FDA/CFSAN, 5100 Paint Branch Parkway, HFS-205 Rm 2D-011, College Park, MD 20740) The most-published designs, three 10-fold dilutions with 3, 5, 8, or 10 tubes at each dilution, are presented here.
References
- Blodgett, R. J. 2005a. Serial dilution with a confirmation step. Food Microbiology22:547-552.
- Blodgett, R. J. 2005b. Upper and lower bounds for a serial dilution test. Journal of the AOAC international88 (4):1227-1230.
- Cochran, W. G. 1950. Estimation of bacterial densities by means of the 'Most Probable Number.' Biometrics6:105-116.
- de Man, J. C. 1983. MPN tables, corrected. Eur. J. Appl. Biotechnol.17:301-305.
- Eisenhart, C., and P. W. Wilson. 1943. Statistical methods and control in bacteriology. Bacteriol. Rev.7:57-137.
- Garthright, W. E. and Blodgett, R.J. 2003, FDA's preferred MPN methods for Standard, large or unusualtests, with a spreadsheet. Food Microbiology20:439-445.
- Garthright, W. E. 1993. Bias in the logarithm of microbial density estimates from serial dilutions. Biom. J. 35: 3:299-314.
- Haldane, J.B.S. 1939. Sampling errors in the determination of bacterial or virus density by the dilution method. J. Hygiene. 39:289-293.
- Halvorson, H. O., and N. R. Ziegler. 1933. Application of statistics to problems in bacteriology. J. Bacteriol.25:101-121; 26:331-339; 26:559-567.
- McCrady, M. H. 1915. The numerical interpretation of fermentation-tube results. J. Infect. Dis.17:183-212.
- Peeler, J. T., G. A. Houghtby, and A. P. Rainosek. 1992. The most probable number technique, Compendium of Methods for the Microbiological Examination of Foods, 3rd Ed., 105-120.
- Thomas, H. A. 1942. Bacterial densities from fermentation tube tests. J. Am. Water Works Assoc.34:572-576.
- Woodward, R. L. 1957. How probable is the most probable number? J. Am. Water Works Assoc.49:1060-1068.
Tables
- Table 5. 10 tubes at 10 ml inocula(Added July 2003)
| Pos. Tubes | MPN/g | Conf. lim. | Pos. tubes | MPN/g | Conf. lim. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.10 | 0.01 | 0.001 | Low | High | 0.10 | 0.01 | 0.001 | Low | High | ||
| 0 | 0 | 0 | <> | – | 9.5 | 2 | 2 | 0 | 21 | 4.5 | 42 |
| 0 | 0 | 1 | 3.0 | 0.15 | 9.6 | 2 | 2 | 1 | 28 | 8.7 | 94 |
| 0 | 1 | 0 | 3.0 | 0.15 | 11 | 2 | 2 | 2 | 35 | 8.7 | 94 |
| 0 | 1 | 1 | 6.1 | 1.2 | 18 | 2 | 3 | 0 | 29 | 8.7 | 94 |
| 0 | 2 | 0 | 6.2 | 1.2 | 18 | 2 | 3 | 1 | 36 | 8.7 | 94 |
| 0 | 3 | 0 | 9.4 | 3.6 | 38 | 3 | 0 | 0 | 23 | 4.6 | 94 |
| 1 | 0 | 0 | 3.6 | 0.17 | 18 | 3 | 0 | 1 | 38 | 8.7 | 110 |
| 1 | 0 | 1 | 7.2 | 1.3 | 18 | 3 | 0 | 2 | 64 | 17 | 180 |
| 1 | 0 | 2 | 11 | 3.6 | 38 | 3 | 1 | 0 | 43 | 9 | 180 |
| 1 | 1 | 0 | 7.4 | 1.3 | 20 | 3 | 1 | 1 | 75 | 17 | 200 |
| 1 | 1 | 1 | 11 | 3.6 | 38 | 3 | 1 | 2 | 120 | 37 | 420 |
| 1 | 2 | 0 | 11 | 3.6 | 42 | 3 | 1 | 3 | 160 | 40 | 420 |
| 1 | 2 | 1 | 15 | 4.5 | 42 | 3 | 2 | 0 | 93 | 18 | 420 |
| 1 | 3 | 0 | 16 | 4.5 | 42 | 3 | 2 | 1 | 150 | 37 | 420 |
| 2 | 0 | 0 | 9.2 | 1.4 | 38 | 3 | 2 | 2 | 210 | 40 | 430 |
| 2 | 0 | 1 | 14 | 3.6 | 42 | 3 | 2 | 3 | 290 | 90 | 1,000 |
| 2 | 0 | 2 | 20 | 4.5 | 42 | 3 | 3 | 0 | 240 | 42 | 1,000 |
| 2 | 1 | 0 | 15 | 3.7 | 42 | 3 | 3 | 1 | 460 | 90 | 2,000 |
| 2 | 1 | 1 | 20 | 4.5 | 42 | 3 | 3 | 2 | 1100 | 180 | 4,100 |
| 2 | 1 | 2 | 27 | 8.7 | 94 | 3 | 3 | 3 | >1100 | 420 | – |
| Pos. Tubes | MPN/g | Conf. lim. | Pos. tubes | MPN/g | Conf. lim. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.01 | 0.001 | Low | High | 0.1 | 0.01 | 0.001 | Low | High | ||
| 0 | 0 | 0 | <> | – | 6.8 | 4 | 0 | 2 | 21 | 6.8 | 40 |
| 0 | 0 | 1 | 1.8 | 0.09 | 6.8 | 4 | 0 | 3 | 25 | 9.8 | 70 |
| 0 | 1 | 0 | 1.8 | 0.09 | 6.9 | 4 | 1 | 0 | 17 | 6 | 40 |
| 0 | 1 | 1 | 3.6 | 0.7 | 10 | 4 | 1 | 1 | 21 | 6.8 | 42 |
| 0 | 2 | 0 | 3.7 | 0.7 | 10 | 4 | 1 | 2 | 26 | 9.8 | 70 |
| 0 | 2 | 1 | 5.5 | 1.8 | 15 | 4 | 1 | 3 | 31 | 10 | 70 |
| 0 | 3 | 0 | 5.6 | 1.8 | 15 | 4 | 2 | 0 | 22 | 6.8 | 50 |
| 1 | 0 | 0 | 2 | 0.1 | 10 | 4 | 2 | 1 | 26 | 9.8 | 70 |
| 1 | 0 | 1 | 4 | 0.7 | 10 | 4 | 2 | 2 | 32 | 10 | 70 |
| 1 | 0 | 2 | 6 | 1.8 | 15 | 4 | 2 | 3 | 38 | 14 | 100 |
| 1 | 1 | 0 | 4 | 0.7 | 12 | 4 | 3 | 0 | 27 | 9.9 | 70 |
| 1 | 1 | 1 | 6.1 | 1.8 | 15 | 4 | 3 | 1 | 33 | 10 | 70 |
| 1 | 1 | 2 | 8.1 | 3.4 | 22 | 4 | 3 | 2 | 39 | 14 | 100 |
| 1 | 2 | 0 | 6.1 | 1.8 | 15 | 4 | 4 | 0 | 34 | 14 | 100 |
| 1 | 2 | 1 | 8.2 | 3.4 | 22 | 4 | 4 | 1 | 40 | 14 | 100 |
| 1 | 3 | 0 | 8.3 | 3.4 | 22 | 4 | 4 | 2 | 47 | 15 | 120 |
| 1 | 3 | 1 | 10 | 3.5 | 22 | 4 | 5 | 0 | 41 | 14 | 100 |
| 1 | 4 | 0 | 11 | 3.5 | 22 | 4 | 5 | 1 | 48 | 15 | 120 |
| 2 | 0 | 0 | 4.5 | 0.79 | 15 | 5 | 0 | 0 | 23 | 6.8 | 70 |
| 2 | 0 | 1 | 6.8 | 1.8 | 15 | 5 | 0 | 1 | 31 | 10 | 70 |
| 2 | 0 | 2 | 9.1 | 3.4 | 22 | 5 | 0 | 2 | 43 | 14 | 100 |
| 2 | 1 | 0 | 6.8 | 1.8 | 17 | 5 | 0 | 3 | 58 | 22 | 150 |
| 2 | 1 | 1 | 9.2 | 3.4 | 22 | 5 | 1 | 0 | 33 | 10 | 100 |
| 2 | 1 | 2 | 12 | 4.1 | 26 | 5 | 1 | 1 | 46 | 14 | 120 |
| 2 | 2 | 0 | 9.3 | 3.4 | 22 | 5 | 1 | 2 | 63 | 22 | 150 |
| 2 | 2 | 1 | 12 | 4.1 | 26 | 5 | 1 | 3 | 84 | 34 | 220 |
| 2 | 2 | 2 | 14 | 5.9 | 36 | 5 | 2 | 0 | 49 | 15 | 150 |
| 2 | 3 | 0 | 12 | 4.1 | 26 | 5 | 2 | 1 | 70 | 22 | 170 |
| 2 | 3 | 1 | 14 | 5.9 | 36 | 5 | 2 | 2 | 94 | 34 | 230 |
| 2 | 4 | 0 | 15 | 5.9 | 36 | 5 | 2 | 3 | 120 | 36 | 250 |
| 3 | 0 | 0 | 7.8 | 2.1 | 22 | 5 | 2 | 4 | 150 | 58 | 400 |
| 3 | 0 | 1 | 11 | 3.5 | 23 | 5 | 3 | 0 | 79 | 22 | 220 |
| 3 | 0 | 2 | 13 | 5.6 | 35 | 5 | 3 | 1 | 110 | 34 | 250 |
| 3 | 1 | 0 | 11 | 3.5 | 26 | 5 | 3 | 2 | 140 | 52 | 400 |
| 3 | 1 | 1 | 14 | 5.6 | 36 | 5 | 3 | 3 | 180 | 70 | 400 |
| 3 | 1 | 2 | 17 | 6 | 36 | 5 | 3 | 4 | 210 | 70 | 400 |
| 3 | 2 | 0 | 14 | 5.7 | 36 | 5 | 4 | 0 | 130 | 36 | 400 |
| 3 | 2 | 1 | 17 | 6.8 | 40 | 5 | 4 | 1 | 170 | 58 | 400 |
| 3 | 2 | 2 | 20 | 6.8 | 40 | 5 | 4 | 2 | 220 | 70 | 440 |
| 3 | 3 | 0 | 17 | 6.8 | 40 | 5 | 4 | 3 | 280 | 100 | 710 |
| 3 | 3 | 1 | 21 | 6.8 | 40 | 5 | 4 | 4 | 350 | 100 | 710 |
| 3 | 3 | 2 | 24 | 9.8 | 70 | 5 | 4 | 5 | 430 | 150 | 1,100 |
| 3 | 4 | 0 | 21 | 6.8 | 40 | 5 | 5 | 0 | 240 | 70 | 710 |
| 3 | 4 | 1 | 24 | 9.8 | 70 | 5 | 5 | 1 | 350 | 100 | 1100 |
| 3 | 5 | 0 | 25 | 9.8 | 70 | 5 | 5 | 2 | 540 | 150 | 1700 |
| 4 | 0 | 0 | 13 | 4.1 | 35 | 5 | 5 | 3 | 920 | 220 | 2600 |
| 4 | 0 | 1 | 17 | 5.9 | 36 | 5 | 5 | 4 | 1600 | 400 | 4600 |
| 5 | 5 | 5 | >1600 | 700 | – | ||||||
| Pos. tubes | MPN/g | Conf. lim. | Pos. tubes | MPN/g | Conf. lim. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.01 | 0.001 | Low | High | 0.1 | 0.01 | 0.001 | Low | High | ||
| 0 | 0 | 0 | <> | – | 3.1 | 8 | 2 | 0 | 17 | 7.7 | 34 |
| 0 | 0 | 1 | 0.9 | 0.04 | 3.1 | 8 | 2 | 1 | 19 | 9 | 34 |
| 0 | 0 | 2 | 1.8 | 0.33 | 5.1 | 8 | 2 | 2 | 21 | 10 | 39 |
| 0 | 1 | 0 | 0.9 | 0.04 | 3.6 | 8 | 2 | 3 | 23 | 11 | 44 |
| 0 | 1 | 1 | 1.8 | 0.33 | 5.1 | 8 | 3 | 0 | 19 | 9 | 34 |
| 0 | 2 | 0 | 1.8 | 0.33 | 5.1 | 8 | 3 | 1 | 21 | 10 | 39 |
| 0 | 2 | 1 | 2.7 | 0.8 | 7.2 | 8 | 3 | 2 | 24 | 11 | 44 |
| 0 | 3 | 0 | 2.7 | 0.8 | 7.2 | 8 | 3 | 3 | 26 | 12 | 50 |
| 1 | 0 | 0 | 0.94 | 0.05 | 5.1 | 8 | 4 | 0 | 22 | 10 | 39 |
| 1 | 0 | 1 | 1.9 | 0.33 | 5.1 | 8 | 4 | 1 | 24 | 11 | 44 |
| 1 | 0 | 2 | 2.8 | 0.8 | 7.2 | 8 | 4 | 2 | 26 | 12 | 50 |
| 1 | 1 | 0 | 1.9 | 0.33 | 5.7 | 8 | 4 | 3 | 29 | 14 | 58 |
| 1 | 1 | 1 | 2.9 | 0.8 | 7.2 | 8 | 5 | 0 | 24 | 11 | 44 |
| 1 | 1 | 2 | 3.8 | 1.4 | 9 | 8 | 5 | 1 | 27 | 12 | 50 |
| 1 | 2 | 0 | 2.9 | 0.8 | 7.2 | 8 | 5 | 2 | 29 | 14 | 58 |
| 1 | 2 | 1 | 3.8 | 1.4 | 9 | 8 | 5 | 3 | 32 | 15 | 62 |
| 1 | 3 | 0 | 3.8 | 1.4 | 9 | 8 | 6 | 0 | 27 | 12 | 50 |
| 1 | 3 | 1 | 4.8 | 2.1 | 11 | 8 | 6 | 1 | 30 | 14 | 58 |
| 1 | 4 | 0 | 4.8 | 2.1 | 11 | 8 | 6 | 2 | 33 | 15 | 62 |
| 2 | 0 | 0 | 2 | 0.37 | 7.2 | 8 | 7 | 0 | 30 | 14 | 58 |
| 2 | 0 | 1 | 3 | 0.81 | 7.3 | 8 | 7 | 1 | 33 | 17 | 73 |
| 2 | 0 | 2 | 4 | 1.4 | 9 | 8 | 7 | 2 | 36 | 17 | 74 |
| 2 | 1 | 0 | 3 | 0.82 | 7.8 | 8 | 8 | 0 | 34 | 17 | 73 |
| 2 | 1 | 1 | 4 | 1.4 | 9 | 8 | 8 | 1 | 37 | 17 | 74 |
| 2 | 1 | 2 | 5 | 2.1 | 11 | 9 | 0 | 0 | 17 | 7.5 | 31 |
| 2 | 2 | 0 | 4 | 1.4 | 9.1 | 9 | 0 | 1 | 19 | 9 | 34 |
| 2 | 2 | 1 | 5 | 2.1 | 11 | 9 | 0 | 2 | 22 | 10 | 39 |
| 2 | 2 | 2 | 6.1 | 3 | 14 | 9 | 0 | 3 | 24 | 11 | 44 |
| 2 | 3 | 0 | 5.1 | 2.1 | 11 | 9 | 1 | 0 | 19 | 9 | 39 |
| 2 | 3 | 1 | 6.1 | 3 | 14 | 9 | 1 | 1 | 22 | 10 | 40 |
| 2 | 4 | 0 | 6.1 | 3 | 14 | 9 | 1 | 2 | 25 | 11 | 44 |
| 2 | 4 | 1 | 7.2 | 3.1 | 15 | 9 | 1 | 3 | 28 | 14 | 58 |
| 2 | 5 | 0 | 7.2 | 3.1 | 15 | 9 | 1 | 4 | 31 | 14 | 58 |
| 3 | 0 | 0 | 3.2 | 0.9 | 9 | 9 | 2 | 0 | 22 | 10 | 44 |
| 3 | 0 | 1 | 4.2 | 1.4 | 9.1 | 9 | 2 | 1 | 25 | 11 | 46 |
| 3 | 0 | 2 | 5.3 | 2.1 | 11 | 9 | 2 | 2 | 28 | 14 | 58 |
| 3 | 1 | 0 | 4.2 | 1.4 | 10 | 9 | 2 | 3 | 32 | 14 | 58 |
| 3 | 1 | 1 | 5.3 | 2.1 | 11 | 9 | 2 | 4 | 35 | 17 | 73 |
| 3 | 1 | 2 | 6.4 | 3 | 14 | 9 | 3 | 0 | 25 | 12 | 50 |
| 3 | 2 | 0 | 5.3 | 2.1 | 12 | 9 | 3 | 1 | 29 | 14 | 58 |
| 3 | 2 | 1 | 6.4 | 3 | 14 | 9 | 3 | 2 | 32 | 15 | 62 |
| 3 | 2 | 2 | 7.5 | 3.1 | 15 | 9 | 3 | 3 | 36 | 17 | 74 |
| 3 | 3 | 0 | 6.5 | 3 | 14 | 9 | 3 | 4 | 40 | 20 | 91 |
| 3 | 3 | 1 | 7.6 | 3.1 | 15 | 9 | 4 | 0 | 29 | 14 | 58 |
| 3 | 3 | 2 | 8.7 | 3.6 | 17 | 9 | 4 | 1 | 33 | 15 | 62 |
| 3 | 4 | 0 | 7.6 | 3.1 | 15 | 9 | 4 | 2 | 37 | 17 | 74 |
| 3 | 4 | 1 | 8.7 | 3.6 | 17 | 9 | 4 | 3 | 41 | 20 | 91 |
| 3 | 5 | 0 | 8.8 | 3.6 | 17 | 9 | 4 | 4 | 45 | 20 | 91 |
| 4 | 0 | 0 | 4.5 | 1.6 | 11 | 9 | 5 | 0 | 33 | 17 | 73 |
| 4 | 0 | 1 | 5.6 | 2.2 | 12 | 9 | 5 | 1 | 37 | 17 | 74 |
| 4 | 0 | 2 | 6.8 | 3 | 14 | 9 | 5 | 2 | 42 | 20 | 91 |
| 4 | 1 | 0 | 5.6 | 2.2 | 12 | 9 | 5 | 3 | 46 | 20 | 91 |
| 4 | 1 | 1 | 6.8 | 3 | 14 | 9 | 5 | 4 | 51 | 25 | 120 |
| 4 | 1 | 2 | 8 | 3.6 | 17 | 9 | 6 | 0 | 38 | 17 | 74 |
| 4 | 2 | 0 | 6.8 | 3 | 15 | 9 | 6 | 1 | 43 | 20 | 91 |
| 4 | 2 | 1 | 8 | 3.6 | 17 | 9 | 6 | 2 | 47 | 21 | 100 |
| 4 | 2 | 2 | 9.2 | 3.7 | 17 | 9 | 6 | 3 | 53 | 25 | 120 |
| 4 | 3 | 0 | 8.1 | 3.6 | 17 | 9 | 7 | 0 | 44 | 20 | 91 |
| 4 | 3 | 1 | 9.3 | 4.5 | 18 | 9 | 7 | 1 | 49 | 21 | 100 |
| 4 | 3 | 2 | 10 | 5 | 20 | 9 | 7 | 2 | 54 | 25 | 120 |
| 4 | 4 | 0 | 9.3 | 4.5 | 18 | 9 | 7 | 3 | 60 | 26 | 120 |
| 4 | 4 | 1 | 11 | 5 | 20 | 9 | 8 | 0 | 50 | 25 | 120 |
| 4 | 5 | 0 | 11 | 5 | 20 | 9 | 8 | 1 | 55 | 25 | 120 |
| 4 | 5 | 1 | 12 | 5.6 | 22 | 9 | 8 | 2 | 61 | 26 | 120 |
| 4 | 6 | 0 | 12 | 5.6 | 22 | 9 | 8 | 3 | 68 | 30 | 140 |
| 5 | 0 | 0 | 6 | 2.5 | 14 | 9 | 9 | 0 | 57 | 25 | 120 |
| 5 | 0 | 1 | 7.2 | 3.1 | 15 | 9 | 9 | 1 | 63 | 30 | 140 |
| 5 | 0 | 2 | 8.5 | 3.6 | 17 | 9 | 9 | 2 | 70 | 30 | 140 |
| 5 | 0 | 3 | 9.8 | 4.5 | 18 | 10 | 0 | 0 | 23 | 11 | 44 |
| 5 | 1 | 0 | 7.3 | 3.1 | 15 | 10 | 0 | 1 | 27 | 12 | 50 |
| 5 | 1 | 1 | 8.5 | 3.6 | 17 | 10 | 0 | 2 | 31 | 14 | 58 |
| 5 | 1 | 2 | 9.8 | 4.5 | 18 | 10 | 0 | 3 | 37 | 17 | 73 |
| 5 | 1 | 3 | 11 | 5 | 21 | 10 | 1 | 0 | 27 | 12 | 57 |
| 5 | 2 | 0 | 8.6 | 3.6 | 17 | 10 | 1 | 1 | 32 | 14 | 61 |
| 5 | 2 | 1 | 9.9 | 4.5 | 18 | 10 | 1 | 2 | 38 | 17 | 74 |
| 5 | 2 | 2 | 11 | 5 | 21 | 10 | 1 | 3 | 44 | 20 | 91 |
| 5 | 3 | 0 | 10 | 4.5 | 18 | 10 | 1 | 4 | 52 | 25 | 120 |
| 5 | 3 | 1 | 11 | 5 | 21 | 10 | 2 | 0 | 33 | 15 | 73 |
| 5 | 3 | 2 | 13 | 5.6 | 23 | 10 | 2 | 1 | 39 | 17 | 79 |
| 5 | 4 | 0 | 11 | 5 | 21 | 10 | 2 | 2 | 46 | 20 | 91 |
| 5 | 4 | 1 | 13 | 5.6 | 23 | 10 | 2 | 3 | 54 | 25 | 120 |
| 5 | 4 | 2 | 14 | 7 | 26 | 10 | 2 | 4 | 63 | 30 | 140 |
| 5 | 5 | 0 | 13 | 6.3 | 25 | 10 | 3 | 0 | 40 | 17 | 91 |
| 5 | 5 | 1 | 14 | 7 | 26 | 10 | 3 | 1 | 47 | 20 | 100 |
| 5 | 6 | 0 | 14 | 7 | 26 | 10 | 3 | 2 | 56 | 25 | 120 |
| 6 | 0 | 0 | 7.8 | 3.1 | 17 | 10 | 3 | 3 | 66 | 30 | 140 |
| 6 | 0 | 1 | 9.2 | 3.6 | 17 | 10 | 3 | 4 | 77 | 34 | 150 |
| 6 | 0 | 2 | 11 | 5 | 20 | 10 | 3 | 5 | 89 | 39 | 180 |
| 6 | 0 | 3 | 12 | 5.6 | 22 | 10 | 4 | 0 | 49 | 21 | 120 |
| 6 | 1 | 0 | 9.2 | 3.7 | 18 | 10 | 4 | 1 | 59 | 25 | 120 |
| 6 | 1 | 1 | 11 | 5 | 21 | 10 | 4 | 2 | 70 | 30 | 150 |
| 6 | 1 | 2 | 12 | 5.6 | 22 | 10 | 4 | 3 | 82 | 38 | 180 |
| 6 | 1 | 3 | 14 | 7 | 26 | 10 | 4 | 4 | 94 | 44 | 180 |
| 6 | 2 | 0 | 11 | 5 | 21 | 10 | 4 | 5 | 110 | 50 | 210 |
| 6 | 2 | 1 | 12 | 5.6 | 22 | 10 | 5 | 0 | 62 | 26 | 140 |
| 6 | 2 | 2 | 14 | 7 | 26 | 10 | 5 | 1 | 74 | 30 | 150 |
| 6 | 2 | 3 | 15 | 7.4 | 30 | 10 | 5 | 2 | 87 | 38 | 180 |
| 6 | 3 | 0 | 12 | 5.6 | 23 | 10 | 5 | 3 | 100 | 44 | 180 |
| 6 | 3 | 1 | 14 | 7 | 26 | 10 | 5 | 4 | 110 | 50 | 210 |
| 6 | 3 | 2 | 15 | 7.4 | 30 | 10 | 5 | 5 | 130 | 57 | 220 |
| 6 | 4 | 0 | 14 | 7 | 26 | 10 | 5 | 6 | 140 | 70 | 280 |
| 6 | 4 | 1 | 15 | 7.4 | 30 | 10 | 6 | 0 | 79 | 34 | 180 |
| 6 | 4 | 2 | 17 | 9 | 34 | 10 | 6 | 1 | 94 | 39 | 180 |
| 6 | 5 | 0 | 16 | 7.4 | 30 | 10 | 6 | 2 | 110 | 50 | 210 |
| 6 | 5 | 1 | 17 | 9 | 34 | 10 | 6 | 3 | 120 | 57 | 220 |
| 6 | 5 | 2 | 19 | 9 | 34 | 10 | 6 | 4 | 140 | 70 | 280 |
| 6 | 6 | 0 | 17 | 9 | 34 | 10 | 6 | 5 | 160 | 74 | 280 |
| 6 | 6 | 1 | 19 | 9 | 34 | 10 | 6 | 6 | 180 | 91 | 350 |
| 6 | 7 | 0 | 19 | 9 | 34 | 10 | 7 | 0 | 100 | 44 | 210 |
| 7 | 0 | 0 | 10 | 4.5 | 20 | 10 | 7 | 1 | 120 | 50 | 220 |
| 7 | 0 | 1 | 12 | 5 | 21 | 10 | 7 | 2 | 140 | 61 | 280 |
| 7 | 0 | 2 | 13 | 6.3 | 25 | 10 | 7 | 3 | 150 | 73 | 280 |
| 7 | 0 | 3 | 15 | 7.2 | 28 | 10 | 7 | 4 | 170 | 91 | 350 |
| 7 | 1 | 0 | 12 | 5 | 22 | 10 | 7 | 5 | 190 | 91 | 350 |
| 7 | 1 | 1 | 13 | 6.3 | 25 | 10 | 7 | 6 | 220 | 100 | 380 |
| 7 | 1 | 2 | 15 | 7.2 | 28 | 10 | 7 | 7 | 240 | 110 | 480 |
| 7 | 1 | 3 | 17 | 7.7 | 31 | 10 | 8 | 0 | 130 | 60 | 250 |
| 7 | 2 | 0 | 13 | 6.4 | 26 | 10 | 8 | 1 | 150 | 70 | 280 |
| 7 | 2 | 1 | 15 | 7.2 | 28 | 10 | 8 | 2 | 170 | 80 | 350 |
| 7 | 2 | 2 | 17 | 7.7 | 31 | 10 | 8 | 3 | 200 | 90 | 350 |
| 7 | 2 | 3 | 19 | 9 | 34 | 10 | 8 | 4 | 220 | 100 | 380 |
| 7 | 3 | 0 | 15 | 7.2 | 30 | 10 | 8 | 5 | 250 | 120 | 480 |
| 7 | 3 | 1 | 17 | 9 | 34 | 10 | 8 | 6 | 280 | 120 | 480 |
| 7 | 3 | 2 | 19 | 9 | 34 | 10 | 8 | 7 | 310 | 150 | 620 |
| 7 | 3 | 3 | 21 | 10 | 39 | 10 | 8 | 8 | 350 | 150 | 620 |
| 7 | 4 | 0 | 17 | 9 | 34 | 10 | 9 | 0 | 170 | 74 | 310 |
| 7 | 4 | 1 | 19 | 9 | 34 | 10 | 9 | 1 | 200 | 91 | 380 |
| 7 | 4 | 2 | 21 | 10 | 39 | 10 | 9 | 2 | 230 | 100 | 480 |
| 7 | 4 | 3 | 23 | 11 | 44 | 10 | 9 | 3 | 260 | 120 | 480 |
| 7 | 5 | 0 | 19 | 9 | 34 | 10 | 9 | 4 | 300 | 140 | 620 |
| 7 | 5 | 1 | 21 | 10 | 39 | 10 | 9 | 5 | 350 | 150 | 630 |
| 7 | 5 | 2 | 23 | 11 | 44 | 10 | 9 | 6 | 400 | 180 | 820 |
| 7 | 6 | 0 | 21 | 10 | 39 | 10 | 9 | 7 | 460 | 210 | 970 |
| 7 | 6 | 1 | 23 | 11 | 44 | 10 | 9 | 8 | 530 | 210 | 970 |
| 7 | 6 | 2 | 25 | 12 | 46 | 10 | 9 | 9 | 610 | 280 | 1300 |
| 7 | 7 | 0 | 23 | 11 | 44 | 10 | 10 | 0 | 240 | 110 | 480 |
| 7 | 7 | 1 | 26 | 12 | 50 | 10 | 10 | 1 | 290 | 120 | 620 |
| 8 | 0 | 0 | 13 | 5.6 | 25 | 10 | 10 | 2 | 350 | 150 | 820 |
| 8 | 0 | 1 | 15 | 7 | 26 | 10 | 10 | 3 | 430 | 180 | 970 |
| 8 | 0 | 2 | 17 | 7.5 | 30 | 10 | 10 | 4 | 540 | 210 | 1300 |
| 8 | 0 | 3 | 19 | 9 | 34 | 10 | 10 | 5 | 700 | 280 | 1500 |
| 8 | 1 | 0 | 15 | 7.1 | 28 | 10 | 10 | 6 | 920 | 350 | 1900 |
| 8 | 1 | 1 | 17 | 7.7 | 31 | 10 | 10 | 7 | 1200 | 480 | 2400 |
| 8 | 1 | 2 | 19 | 9 | 34 | 10 | 10 | 8 | 1600 | 620 | 3400 |
| 8 | 1 | 3 | 21 | 10 | 39 | 10 | 10 | 9 | 2300 | 810 | 5300 |
| 10 | 10 | 10 | >2300 | 1300 | – | ||||||
Table 4. For 8 tubes each at 0.1, 0.01, and 0.001 g inocula,
the MPNs per gram and 95 percent confidence intervals.
| Pos. tubes | MPN/g | conf. lim. | |||
|---|---|---|---|---|---|
| 0.10 | 0.01 | 0.001 | Low | High | |
| 0 | 0 | 0 | <> | – | 4.3 |
| 0 | 0 | 1 | 1.1 | .057 | 4.3 |
| 0 | 0 | 2 | 2.3 | .42 | 6.7 |
| 0 | 1 | 0 | 1.1 | .058 | 4.4 |
| 0 | 1 | 1 | 2.3 | .42 | 6.7 |
| 0 | 2 | 0 | 2.3 | .42 | 6.7 |
| 0 | 2 | 1 | 3.4 | 1.0 | 9.1 |
| 0 | 3 | 0 | 3.4 | 1.0 | 9.1 |
| 1 | 0 | 0 | 1.2 | .064 | 6.7 |
| 1 | 0 | 1 | 2.4 | .42 | 6.8 |
| 1 | 0 | 2 | 3.6 | 1.0 | 9.1 |
| 1 | 1 | 0 | 2.4 | .42 | 7.3 |
| 1 | 1 | 1 | 3.6 | 1.0 | 9.1 |
| 1 | 1 | 2 | 4.8 | 1.8 | 12 |
| 1 | 2 | 0 | 3.6 | 1.0 | 9.1 |
| 1 | 2 | 1 | 4.9 | 1.8 | 12 |
| 1 | 3 | 0 | 4.9 | 1.8 | 12 |
| 1 | 3 | 1 | 6.1 | 2.8 | 15 |
| 1 | 4 | 0 | 6.2 | 2.8 | 15 |
| 2 | 0 | 0 | 2.6 | .47 | 9.1 |
| 2 | 0 | 1 | 3.8 | 1.0 | 9.1 |
| 2 | 0 | 2 | 5.1 | 1.8 | 12 |
| 2 | 1 | 0 | 3.9 | 1.0 | 9.9 |
| 2 | 1 | 1 | 5.2 | 1.8 | 12 |
| 2 | 1 | 2 | 6.5 | 2.8 | 15 |
| 2 | 2 | 0 | 5.2 | 1.8 | 12 |
| 2 | 2 | 1 | 6.5 | 2.8 | 15 |
| 2 | 2 | 2 | 7.9 | 3.3 | 18 |
| 2 | 3 | 0 | 6.6 | 2.8 | 15 |
| 2 | 3 | 1 | 7.9 | 3.3 | 18 |
| 2 | 4 | 0 | 8.0 | 3.3 | 18 |
| 2 | 5 | 0 | 9.4 | 4.3 | 19 |
| 3 | 0 | 0 | 4.1 | 1.2 | 12 |
| 3 | 0 | 1 | 5.5 | 1.9 | 12 |
| 3 | 0 | 2 | 6.9 | 2.8 | 15 |
| 3 | 1 | 0 | 5.6 | 1.9 | 13 |
| 3 | 1 | 1 | 7.0 | 2.8 | 15 |
| 3 | 1 | 2 | 8.4 | 4.0 | 18 |
| 3 | 2 | 0 | 7.0 | 2.9 | 15 |
| 3 | 2 | 1 | 8.5 | 4.0 | 18 |
| 3 | 2 | 2 | 10 | 4.3 | 19 |
| 3 | 3 | 0 | 8.6 | 4.0 | 18 |
| 3 | 3 | 1 | 10 | 4.3 | 19 |
| 3 | 3 | 2 | 12 | 5.2 | 24 |
| 3 | 4 | 0 | 10 | 4.3 | 19 |
| 3 | 4 | 1 | 12 | 5.2 | 24 |
| 3 | 5 | 0 | 12 | 5.2 | 24 |
| 4 | 0 | 0 | 6.0 | 2.1 | 15 |
| 4 | 0 | 1 | 7.5 | 2.9 | 15 |
| 4 | 0 | 2 | 9.1 | 4.1 | 18 |
| 4 | 1 | 0 | 7.6 | 2.9 | 18 |
| 4 | 1 | 1 | 9.2 | 4.1 | 19 |
| 4 | 1 | 2 | 11 | 4.3 | 22 |
| 4 | 2 | 0 | 9.3 | 4.1 | 19 |
| 4 | 2 | 1 | 11 | 4.3 | 22 |
| 4 | 2 | 2 | 13 | 5.7 | 24 |
| 4 | 3 | 0 | 11 | 4.3 | 22 |
| 4 | 3 | 1 | 13 | 5.7 | 24 |
| 4 | 3 | 2 | 14 | 6.6 | 28 |
| 4 | 4 | 0 | 13 | 5.7 | 24 |
| 4 | 4 | 1 | 15 | 6.6 | 29 |
| 4 | 5 | 0 | 15 | 6.6 | 29 |
| 4 | 5 | 1 | 16 | 7.2 | 33 |
| 4 | 6 | 0 | 17 | 7.2 | 33 |
| 5 | 0 | 0 | 8.3 | 3.3 | 18 |
| 5 | 0 | 1 | 10 | 4.3 | 19 |
| 5 | 0 | 2 | 12 | 5.2 | 24 |
| 5 | 0 | 3 | 14 | 6.6 | 29 |
| 5 | 1 | 0 | 10 | 4.3 | 22 |
| 5 | 1 | 1 | 12 | 5.2 | 24 |
| 5 | 1 | 2 | 14 | 6.6 | 29 |
| 5 | 1 | 3 | 16 | 6.7 | 32 |
| 5 | 2 | 0 | 12 | 5.3 | 24 |
| 5 | 2 | 1 | 14 | 6.6 | 29 |
| 5 | 2 | 2 | 16 | 7.2 | 33 |
| 5 | 2 | 3 | 18 | 7.2 | 33 |
| 5 | 3 | 0 | 14 | 6.6 | 29 |
| 5 | 3 | 1 | 16 | 7.2 | 33 |
| 5 | 3 | 2 | 18 | 7.2 | 33 |
| 5 | 4 | 0 | 16 | 7.2 | 33 |
| 5 | 4 | 1 | 18 | 7.6 | 33 |
| 5 | 4 | 2 | 21 | 9.0 | 39 |
| 5 | 5 | 0 | 19 | 7.6 | 33 |
| 5 | 5 | 1 | 21 | 9.0 | 39 |
| 5 | 6 | 0 | 21 | 9.0 | 39 |
| 6 | 0 | 0 | 11 | 4.3 | 24 |
| 6 | 0 | 1 | 13 | 5.7 | 25 |
| 6 | 0 | 2 | 16 | 6.6 | 32 |
| 6 | 0 | 3 | 18 | 7.2 | 33 |
| 6 | 1 | 0 | 14 | 5.8 | 29 |
| 6 | 1 | 1 | 16 | 6.6 | 32 |
| 6 | 1 | 2 | 18 | 7.2 | 33 |
| 6 | 1 | 3 | 21 | 9.0 | 39 |
| 6 | 2 | 0 | 16 | 6.7 | 33 |
| 6 | 2 | 1 | 18 | 7.4 | 33 |
| 6 | 2 | 2 | 21 | 9.0 | 39 |
| 6 | 2 | 3 | 23 | 11 | 50 |
| 6 | 3 | 0 | 19 | 7.6 | 35 |
| 6 | 3 | 1 | 21 | 9.0 | 39 |
| 6 | 3 | 2 | 24 | 11 | 50 |
| 6 | 3 | 3 | 27 | 12 | 53 |
| 6 | 4 | 0 | 21 | 9.0 | 40 |
| 6 | 4 | 1 | 24 | 11 | 50 |
| 6 | 4 | 2 | 27 | 12 | 53 |
| 6 | 6 | 1 | 31 | 13 | 69 |
| 6 | 7 | 0 | 31 | 13 | 69 |
| 7 | 0 | 0 | 16 | 6.6 | 32 |
| 7 | 0 | 1 | 18 | 7.2 | 33 |
| 7 | 0 | 2 | 21 | 9.0 | 40 |
| 7 | 0 | 3 | 25 | 11 | 50 |
| 7 | 1 | 0 | 19 | 7.9 | 39 |
| 7 | 1 | 1 | 22 | 9.0 | 40 |
| 7 | 1 | 2 | 25 | 11 | 50 |
| 7 | 1 | 3 | 29 | 12 | 54 |
| 7 | 2 | 0 | 22 | 9.0 | 45 |
| 7 | 2 | 1 | 25 | 11 | 51 |
| 7 | 2 | 2 | 29 | 13 | 68 |
| 7 | 2 | 3 | 33 | 13 | 69 |
| 7 | 3 | 0 | 26 | 11 | 53 |
| 7 | 3 | 1 | 30 | 13 | 68 |
| 7 | 3 | 2 | 34 | 13 | 69 |
| 7 | 3 | 3 | 39 | 17 | 91 |
| 7 | 4 | 0 | 30 | 13 | 69 |
| 7 | 4 | 1 | 35 | 13 | 69 |
| 7 | 4 | 2 | 39 | 17 | 91 |
| 7 | 4 | 3 | 45 | 18 | 101 |
| 7 | 5 | 0 | 36 | 14 | 75 |
| 7 | 5 | 1 | 40 | 17 | 91 |
| 7 | 5 | 2 | 46 | 18 | 101 |
| 7 | 5 | 3 | 52 | 21 | 117 |
| 7 | 6 | 0 | 41 | 17 | 91 |
| 7 | 6 | 1 | 47 | 21 | 117 |
| 7 | 6 | 2 | 53 | 21 | 117 |
| 7 | 6 | 3 | 59 | 24 | 146 |
| 7 | 7 | 0 | 48 | 21 | 117 |
| 7 | 7 | 1 | 55 | 21 | 117 |
| 7 | 7 | 2 | 61 | 24 | 146 |
| 7 | 8 | 0 | 56 | 21 | 119 |
| 8 | 0 | 0 | 23 | 9.7 | 50 |
| 8 | 0 | 1 | 28 | 12 | 54 |
| 8 | 0 | 2 | 34 | 13 | 69 |
| 8 | 0 | 3 | 41 | 17 | 91 |
| 8 | 1 | 0 | 29 | 12 | 68 |
| 8 | 1 | 1 | 35 | 13 | 75 |
| 8 | 1 | 2 | 43 | 17 | 91 |
| 8 | 1 | 3 | 52 | 21 | 120 |
| 8 | 1 | 4 | 63 | 28 | 150 |
| 8 | 2 | 0 | 36 | 14 | 91 |
| 8 | 2 | 1 | 45 | 17 | 100 |
| 8 | 2 | 2 | 55 | 21 | 120 |
| 8 | 2 | 3 | 67 | 28 | 150 |
| 8 | 2 | 4 | 81 | 32 | 190 |
| 8 | 3 | 0 | 47 | 18 | 120 |
| 8 | 3 | 1 | 58 | 21 | 150 |
| 8 | 3 | 2 | 72 | 28 | 150 |
| 8 | 3 | 3 | 87 | 39 | 190 |
| 8 | 3 | 4 | 102 | 39 | 190 |
| 8 | 3 | 5 | 118 | 50 | 240 |
| 8 | 4 | 0 | 62 | 24 | 150 |
| 8 | 4 | 1 | 77 | 28 | 190 |
| 8 | 4 | 2 | 94 | 39 | 190 |
| 8 | 4 | 3 | 110 | 44 | 220 |
| 8 | 4 | 4 | 130 | 53 | 250 |
| 8 | 4 | 5 | 150 | 68 | 280 |
| 8 | 5 | 0 | 84 | 32 | 190 |
| 8 | 5 | 1 | 100 | 39 | 220 |
| 8 | 5 | 2 | 120 | 50 | 250 |
| 8 | 5 | 3 | 140 | 67 | 280 |
| 8 | 5 | 4 | 170 | 74 | 340 |
| 8 | 5 | 5 | 190 | 74 | 340 |
| 8 | 5 | 6 | 210 | 90 | 400 |
| 8 | 6 | 0 | 110 | 45 | 240 |
| 8 | 6 | 1 | 140 | 53 | 280 |
| 8 | 6 | 2 | 160 | 68 | 340 |
| 8 | 6 | 3 | 190 | 74 | 340 |
| 8 | 6 | 4 | 220 | 90 | 400 |
| 8 | 6 | 5 | 250 | 120 | 490 |
| 8 | 6 | 6 | 290 | 120 | 520 |
| 8 | 7 | 0 | 160 | 68 | 340 |
| 8 | 7 | 1 | 190 | 74 | 400 |
| 8 | 7 | 2 | 230 | 90 | 490 |
| 8 | 7 | 3 | 270 | 116 | 520 |
| 8 | 7 | 4 | 310 | 150 | 710 |
| 8 | 7 | 5 | 370 | 150 | 720 |
| 8 | 7 | 6 | 430 | 190 | 1000 |
| 8 | 7 | 7 | 510 | 190 | 1000 |
| 8 | 8 | 0 | 240 | 99 | 490 |
| 8 | 8 | 1 | 300 | 120 | 710 |
| 8 | 8 | 2 | 380 | 150 | 1000 |
| 8 | 8 | 3 | 510.0 | 190 | 1200 |
| 8 | 8 | 4 | 700 | 240 | 1700 |
| 8 | 8 | 5 | 980 | 340 | 2200 |
| 8 | 8 | 6 | 1400 | 490 | 3100 |
| 8 | 8 | 7 | 2100 | 710 | 5100 |
| 8 | 8 | 8 | >2100 | 1000 | – |
(Added July 2003)
| Pos. tubes | MPN/100ml | Conf. lim. | |
|---|---|---|---|
| Low | High | ||
| 0 | <> | – | 3.3 |
| 1 | 1.1 | .05 | 5.9 |
| 2 | 2.2 | .37 | 8.1 |
| 3 | 3.6 | .91 | 9.7 |
| 4 | 5.1 | 1.6 | 13 |
| 5 | 6.9 | 2.5 | 15 |
| 6 | 9.2 | 3.3 | 19 |
| 7 | 12 | 4.8 | 24 |
| 8 | 16 | 5.9 | 33 |
| 9 | 23 | 8.1 | 53 |
| 10 | >23 | 12 | – |
(Added July 2003)
Serial Dilution Method Procedure Pdf
Download an Excel spreadsheet to calculate values (zip file).
Note: The confidence intervals of the spreadsheet and the tables associated with this appendix may be different. The MPN Excel spreadsheet uses a normal approximation to the log (MPN) to calculate its confidence intervals. This approximation is similar to a normal approximation discussed in Haldane (1939). This approximation is less computationally intense so more appropriate for a spreadsheet than de Man's confidence intervals.
Serial Dilution Standard Procedure
Hypertext Source: BAM 8th Edition, Modified from Revision A CD ROM version 1998 on 6/21/2000.